Fixed Point and B Numbers

MotoHawk Fixed-Point Values and B-Numbers

Generally, when designing algorithms, it can help to know a little about how the intended target computer processes certain instructions. This is especially true with embedded control applications, because different target processors can have significantly different processing capabilities.

To this point, a target computer may or may not have a device called a floating-point unit (FPU) that can perform floating-point mathematics very quickly. If the target does not have this FPU, it would not natively support floating-point operations; instead, any floating-point operations would have to be emulated entirely in software and thus would consume demonstrably more precious memory and/or processing time.

The algorithm designer will want to be aware of the respective processing capabilities or limitations of the target, and to design accordingly to avoid allocating the extra memory and/or processing time. The proper use of basic fixed-point techniques with simple mathematical operations (addition, multiplication, Boolean, etc.), for example, can have a dramatic impact on the efficiency of an application when no FPU is available.

The intent here is to discuss relevant factors in taking processor type into consideration, to address the use of fixed-point vs. floating-point mathematics and algorithms, and to describe the use of fixed point operations and "B-Numbers," in particular, should this be called for.

Fixed-Point vs. Floating-Point Targets

The term “fixed-point” often refers to the decimal point being in a fixed location for a given mathematical operation; conversely, “floating-point” implies a variable decimal-point location.

As stated above, some processors have the on-board FPU to perform floating-point mathematics very quickly; others do not, so any floating-point operations can consume demonstrably more memory and/or processing time. Determine which processor type you are targeting, and then consider whether to use fixed-point or floating-point:

• Floating-point computations are extremely computationally expensive on a fixed-point processor (no FPU).
• On a floating-point processor, floating-point operations are more efficient with respect to the number of necessary steps (no need to apply scales, offsets, rounding, etc.).
• Fixed-point data types, of 2 bytes or less, use fewer resources (flash, RAM, EEPROM, etc.) than floating-point data types (which are at least 4 bytes).
• Floating point can be more convenient and enable quicker development, testing, and debugging (no need to protect for rollover, track scaling and offsets, etc.).

Other factors would include assessment of whether the application is or may become large enough to necessitate use of fixed-point methods to avoid overtaxing the hardware, and whether the target processor hardware might be changed over time and thus add or remove the necessity of fixed-point methods.

Designing for Fixed-Point Targets

When developing for a fixed-point processor, the application is limited to integer data types (uint8, int32, etc.). However, there are techniques for managing a decimal points and resolution within a fixed-point algorithm; at some level, all of these approaches employ a gain and offset to translate the raw integer value to an engineering value that the user will observe in MotoTune. One approach uses a binary gain in conjunction with a so-called “B-Number.”

B-Numbers: A Fixed-Point Approach

MotoHawk includes a block set intended to perform fixed-point operations, using a particular property called B-Numbers. Currently, all MotoHawk Fixed Point B-Number blocks have output data types of int16. Each B-Number corresponds to a unique resolution (2^BNum / 65536) and range (spanning 65536 possible raw values) as in the table below. Note that there is no offset, so there is a trade-off on resolution for a larger range.

16-Bit Scaling
B-Num	Min Value	Max Value	Range	Resolution
-10	-0.000976563	0.000976533	0.001953095	0.000000029802322
-9	-0.001953125	0.001953065	0.00390619	0.000000059604645
-8	-0.00390625	0.003906131	0.007812381	0.000000119209290
-7	-0.0078125	0.007812262	0.015624762	0.000000238418579
-6	-0.015625	0.015624523	0.031249523	0.000000476837158
-5	-0.03125	0.031249046	0.062499046	0.000000953674316
-4	-0.0625	0.062498093	0.124998093	0.000001907348633
-3	-0.125	0.124996185	0.249996185	0.000003814697266
-2	-0.25	0.249992371	0.499992371	0.000007629394531
-1	-0.5	0.499984741	0.999984741	0.000015258789063
0	-1	0.999969482	1.999969482	0.000030517578125
1	-2	1.999938965	3.999938965	0.00006103515625
2	-4	3.99987793	7.99987793	0.0001220703125
3	-8	7.999755859	15.99975586	0.000244140625
4	-16	15.99951172	31.99951172	0.00048828125
5	-32	31.99902344	63.99902344	0.0009765625
6	-64	63.99804688	127.9980469	0.001953125
7	-128	127.9960938	255.9960938	0.00390625
8	-256	255.9921875	511.9921875	0.0078125
9	-512	511.984375	1023.984375	0.015625
10	-1024	1023.96875	2047.96875	0.03125
11	-2048	2047.9375	4095.9375	0.0625
12	-4096	4095.875	8191.875	0.125
13	-8192	8191.75	16383.75	0.25
14	-16384	16383.5	32767.5	0.5
15	-32768	32767	65535	1
16	-65536	65534	131070	2
17	-131072	131068	262140	4
18	-262144	262136	524280	8
19	-524288	524272	1048560	16
20	-1048576	1048544	2097120	32
21	-2097152	2097088	4194240	64
22	-4194304	4194176	8388480	128
23	-8388608	8388352	16776960	256
24	-16777216	16776704	33553920	512
25	-33554432	33553408	67107840	1024

As mentioned previously, each range has 16-bit resolution that is equal to 2^BNum / 65536; thus, the scaling is of a binary type. One advantage of binary scaling over other absolute scalings is that the mathematical operations (as described subsequently) include multiplying/dividing by 2^N factors, which are actually left/right bit shifts and complete faster on the microprocessor than integer multiplies/divides. Another advantage of binary scaling in conjunction with the B-Number method is that certain rules are created that assists the application engineer in mathematical operations and preventing overflow.

Operation Rules

In order to use fixed points for math operations, certain rules apply:

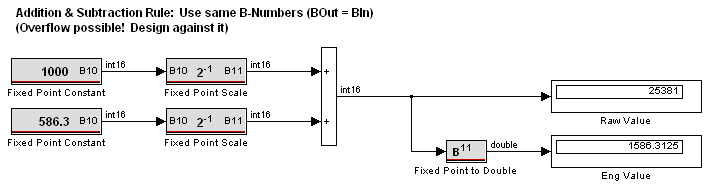
• Addition / Subtraction: To add/subtract, ensure the operands have the same B-Number. Note that overflow may occur; unless the design inherently prevents overflow, use a MotoHawk Fixed Point Scale block to pre-shift the operands to a higher B-Number (to increase range) prior to the operation.
  
  
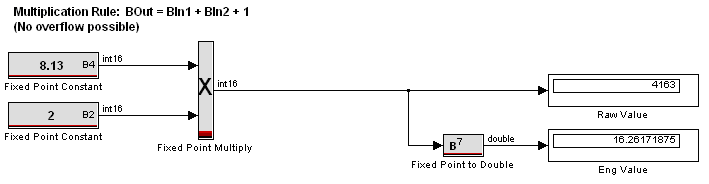
• Multiplication (using a Motohawk Fixed Point Multiply block): The result has a B-Number equal to the sum of the B-Numbers of the operands, plus 1. Note that this rule inherently protects against overflow; no pre-shifting is necessary.
  
  
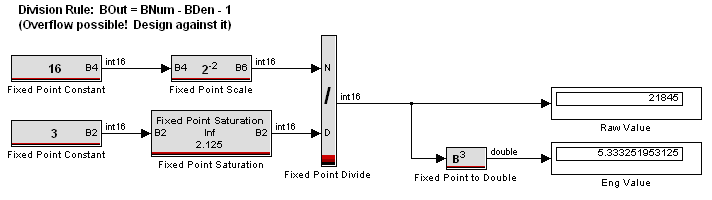
• Division (using a MotoHawk Fixed Point Division block): The result has a B-Number equal to the difference between the B-Numbers of the numerator and the denominator, minus 1. Note that because the denominator can approach or equal 0, overflow may occur; the design must protect against this by limiting the minimum value of the denominator and/or using a MotoHawk Fixed Point Scale block to pre-shift the numerator to a higher B-Number prior to the operation.
  
  
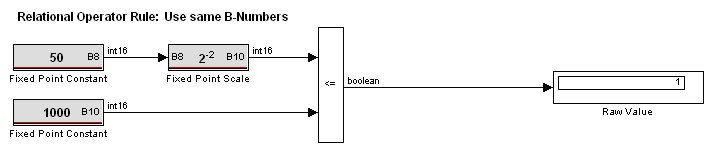
• Relational Operators: When using relational operators, ensure the operands have the same B-Number.